卷积是分析数学中一种重要的运算。设:$f(x)$,$g(x)$是R上的两个可积函数,作积分: $$f(x)∗g(x)=\int_ {-\infty} ^{+\infty} f(τ)g(x−τ)dτ$$
一维卷积
查了很多资料,感觉这篇讲的比较好理解.
对于初学者,我推荐用复利的例子来理解卷积可能更好理解一些:
小明存入100元钱,年利率是5%,按复利计算(即将每一年所获利息加入本金,以计算下一年的利息),那么在五年之后他能拿到的钱数是100(1+5%)^5,如下表所示:

将这笔钱存入银行的一年之后,小明又往银行中存入了100元钱,年利率仍为5%,那么这笔钱按复利计算,到了第五年,将收回的钱数是100(1+5%)^4,我们将这一结果作为新的一行加入上面的表格中:

以此类推,如果小明每年都往银行中存入新的100元钱,那么这个收益表格将是这样的:
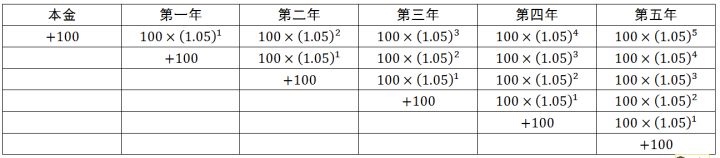
可见,最终小明拿到的钱将等于他各年存入的钱分别计算复利之后得到的钱数的总和,即:

用求和符号来简化这个公式,可以得到: $$\sum_{i=0}^{5}{f(i)g(5-i)}, \mathrm{where} \ f(i)=100, g(5-i) = (1.05)^{5-i}$$ 在上式中,$f(i)$为小明的存钱函数,而$g(i)$为存入银行的每一笔钱的复利计算函数。在这里,小明最终得到的钱就是他的存钱函数和复利计算函数的卷积。 为了更清晰地看到这一点,我们将这个公式推广到连续的情况,也就是说,小明在从0到t的这一段时间内,每时每刻都往银行里存钱,他的存钱函数为$f(\tau)\ (0\leq \tau\leq t)$,而银行也对他存入的每一笔钱按复利公式计算收益:$g(t-\tau)=(1+5%)^{t-\tau}$,则小明到时间t将得到的总钱数为: $$\int_{0}^{t} f(\tau)g(t-\tau)d\tau=\int_{0}^{t} f(\tau)(1+5%)^{t-\tau}d\tau$$ 这也就是卷积的表达式了,上式可以记为(f\ast g)(t)。 相信通过上面这个例子,大家应该能够很清晰地记住卷积公式了。下面我们再展开说两句: 如果我们将小明的存款函数视为一个信号发生(也就是激励)的过程,而将复利函数g(t-\tau)视为一个系统对信号的响应函数(也就是响应),那么二者的卷积$(f\ast g)(t)$就可以看做是在t时刻对系统进行观察,得到的观察结果(也就是输出)将是过去产生的所有信号经过系统的「处理/响应」后得到的结果的叠加,这也就是卷积的物理意义了。
以上为转载,原文地址:如何通俗易懂地解释卷积? - 果程C的回答 - 知乎https://www.zhihu.com/question/22298352/answer/50940942
二维卷积
二维卷积就是一维卷积的扩展,原理差不多。核心还是(反转),移动,乘积,求和。这里二维的反转就是将卷积核沿反对角线翻转,比如:
$$\left[
\begin{matrix}
a & b & c \\
d & e & f \\
g & h & i \\
\end{matrix}
\right] 翻转为
\left[
\begin{matrix}
i & h & g \\
f & e & d \\
c & b & a \\
\end{matrix}
\right] $$
之后,卷积核在二维平面上平移,并且卷积核的每个元素与被卷积图像对应位置相乘,再求和。通过卷积核的不断移动,我们就有了一个新的图像,这个图像完全由卷积核在各个位置时的乘积求和的结果组成。
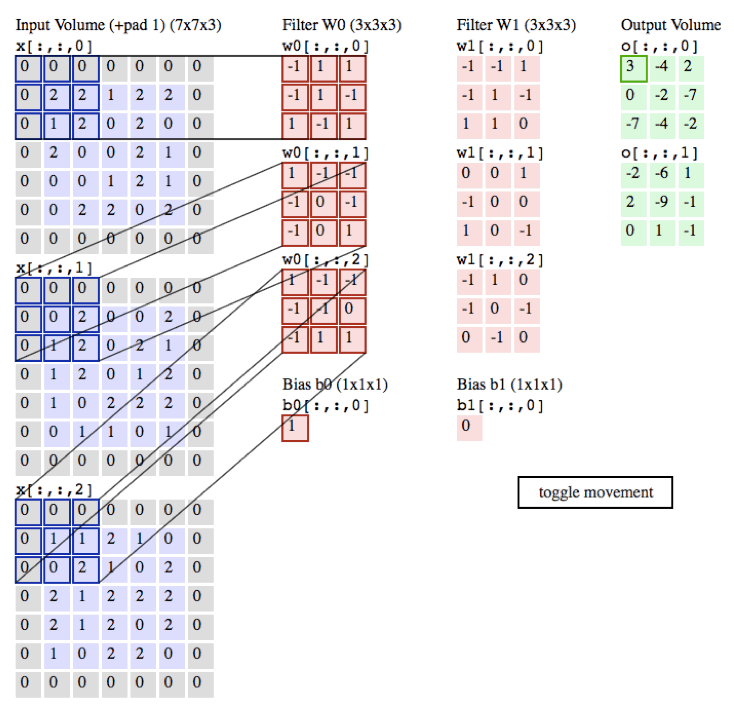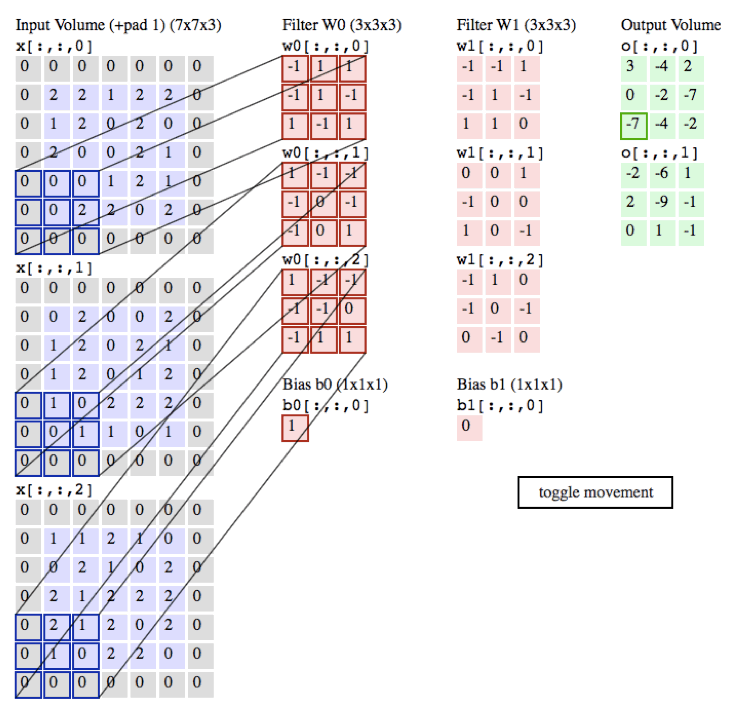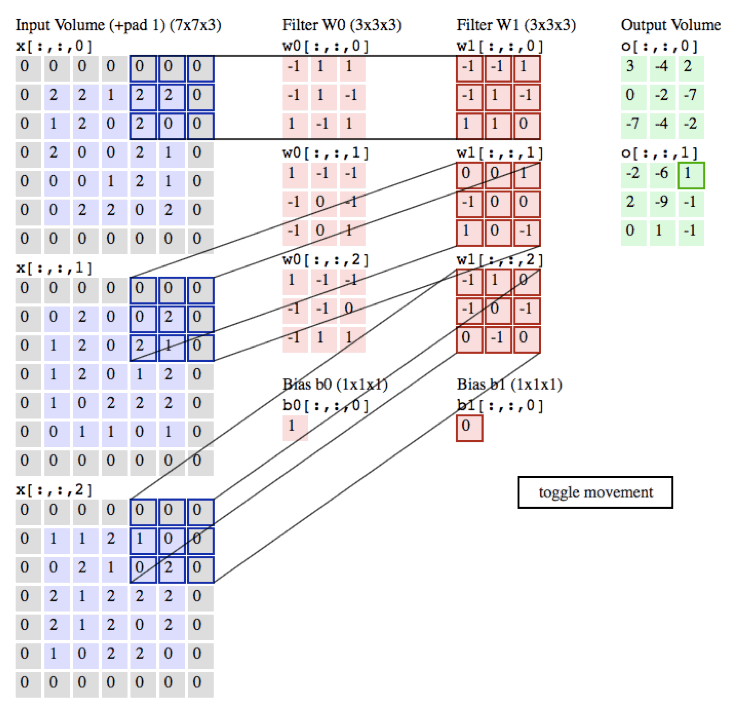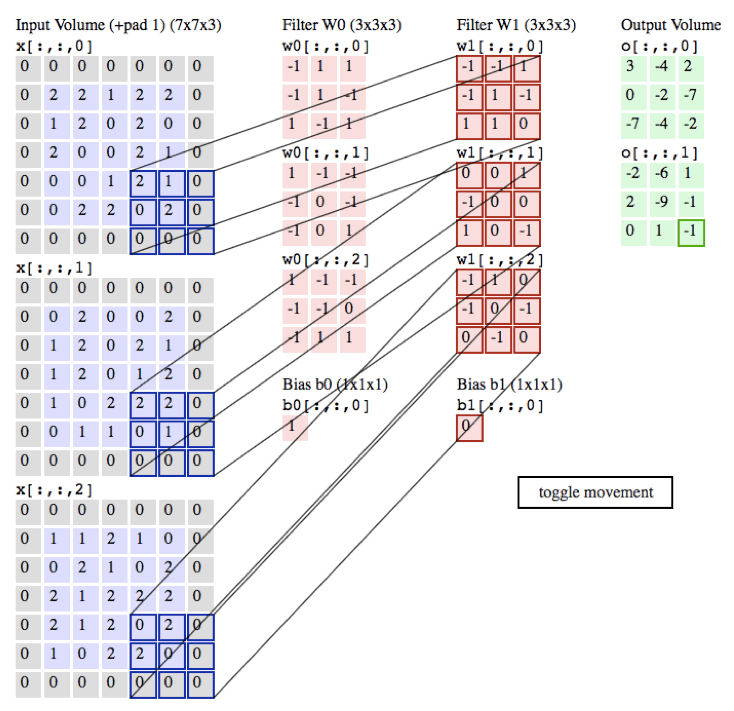
下图给卷积加权迭代的实现过程。

下图以输入为2个通道宽高分别为5的输入、3*3的卷积核、1个通道宽高分别为5的输出,作为一个例子
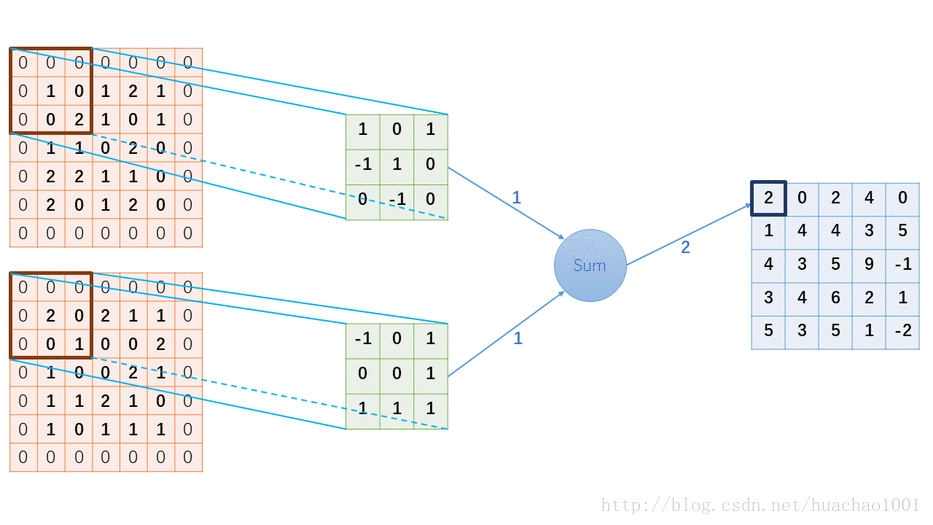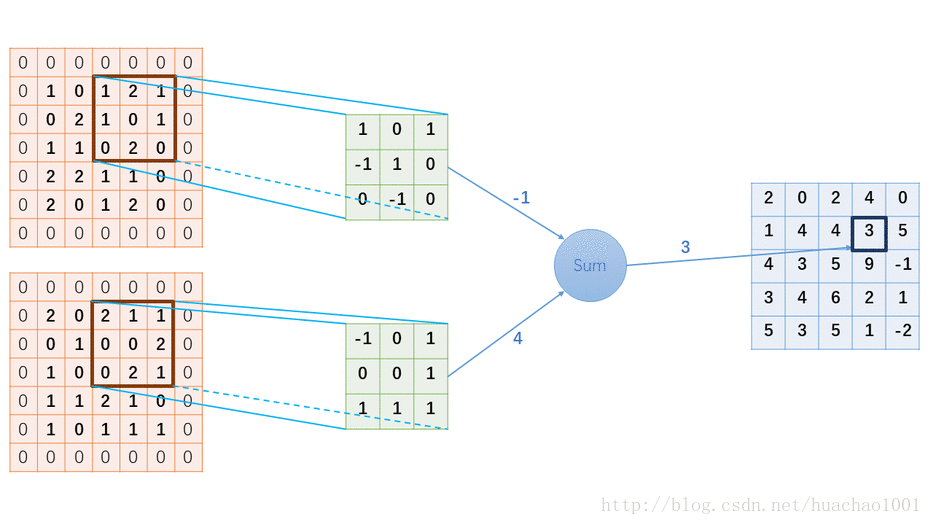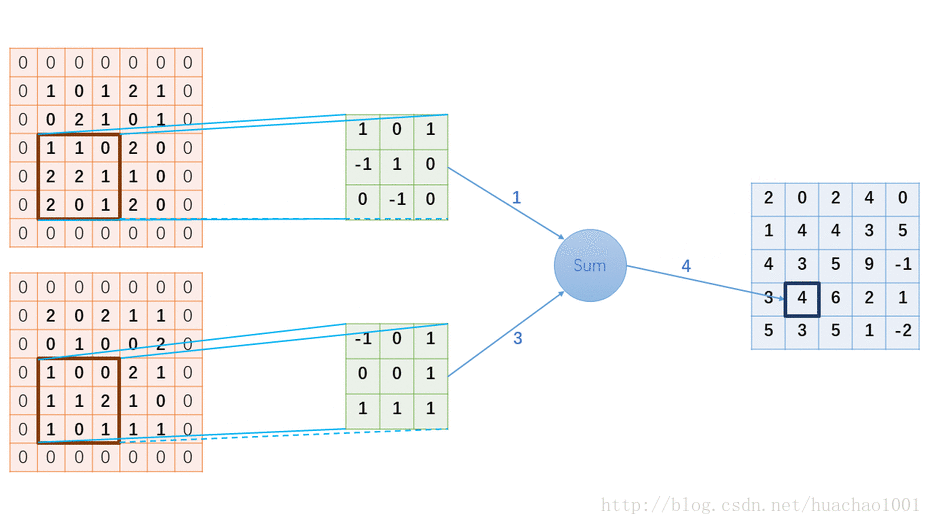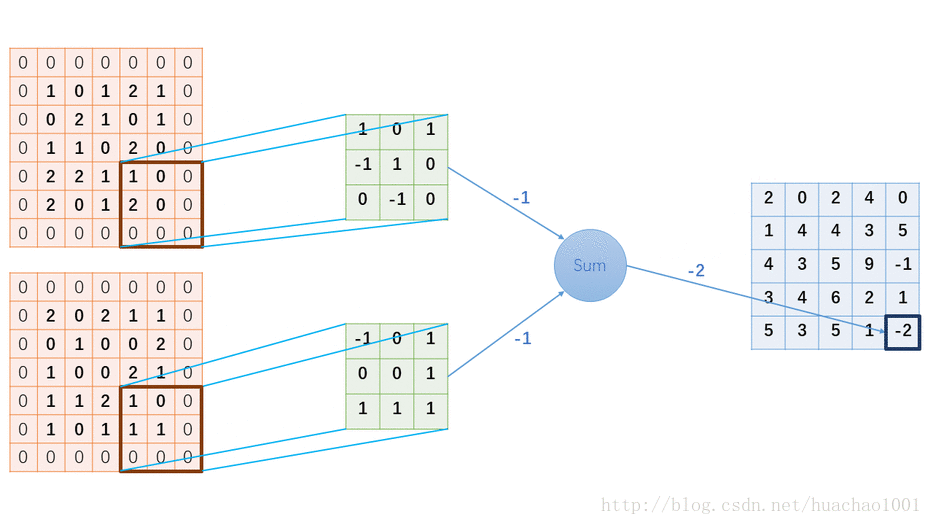
##卷积层尺寸的计算原理 输入矩阵格式:四个维度,依次为:样本数、图像高度、图像宽度、图像通道数 输出矩阵格式:与输出矩阵的维度顺序和含义相同,但是后三个维度(图像高度、图像宽度、图像通道数)的尺寸发生变化。 权重矩阵(卷积核)格式:同样是四个维度,但维度的含义与上面两者都不同,为:卷积核高度、卷积核宽度、输入通道数、输出通道数(卷积核个数) 输入矩阵、权重矩阵、输出矩阵这三者之间的相互决定关系 卷积核的输入通道数(in depth)由输入矩阵的通道数所决定。 输出矩阵的通道数(out depth)由卷积核的输出通道数所决定。 输出矩阵的高度和宽度(height, width)这两个维度的尺寸由输入矩阵、卷积核、扫描方式所共同决定。计算公式如下。 计算padding数值时,VALID=0、SAME=1. $$\begin{cases} height_{out} &= (height_{in} - height_{kernel} + 2 * padding) ~ / ~ stride + 1\[2ex] width_{out} &= (width_{in} - width_{kernel} + 2 * padding) ~ / ~ stride + 1 \end{cases}$$
| 参数名 | 必选 | 类型 | 说明 |
|---|---|---|---|
| input | 是 | tensor | 是一个 4 维的 tensor,即 [ batch, in_height, in_width, in_channels ](若 input 是图像,[ 训练时一个 batch 的图片数量, 图片高度, 图片宽度, 图像通道数 ]) |
| filter | 是 | tensor | 是一个 4 维的 tensor,即 [ filter_height, filter_width, in_channels, out_channels ](若 input 是图像,[ 卷积核的高度,卷积核的宽度,图像通道数,卷积核个数 ]),filter 的 in_channels 必须和 input 的 in_channels 相等 |
| strides | 是 | 列表 | 长度为 4 的 list,卷积时候在 input 上每一维的步长,一般 strides[0] = strides[3] = 1 |
| padding | 是 | string | 只能为 " VALID “,” SAME " 中之一,这个值决定了不同的卷积方式。VALID 丢弃方式;SAME:补全方式 |
| use_cudnn_on_gpu | 否 | bool | 是否使用 cudnn 加速,默认为 true |
| data_format | 否 | string | 只能是 " NHWC “, " NCHW “,默认 " NHWC " |
| name | 否 | string | 运算名称 |
下图为三个特征图,两组卷积核,输出两个特征图的过程。